By Dr. Athanasios Staveris-Polykalas
Artificial intelligence has been revolutionized by the advent of Generative Pretrained Transformer (GPT) models. These models, with their ability to generate human-like text, have been making significant strides in the field of natural language processing. But what’s the secret behind their success? Let’s take a deeper dive into the mathematics that powers these models.
Hallucination: A Quirk in the System
Despite their impressive performance, GPT models are known to exhibit a phenomenon called hallucination. This is when they generate outputs that don’t quite align with the context or are inconsistent with the real world. This can be likened to a well-intentioned storyteller who, in an attempt to make the story more interesting, veers off into a tangent that doesn’t quite fit the narrative.
The hallucination phenomenon is attributed to the model’s inherent limitations, particularly its inability to discern when there is no well-defined correct answer for a given input. As a result, GPT models can generate outputs that deviate from the expected output based on the input context and the true data distribution.
Balancing Hallucination and Creativity
Investigation into the hallucination phenomenon in GPT models reveals a fundamental trade-off between hallucination and creativity. Think of it as a balancing act between a vivid imagination and staying true to the facts. To understand this trade-off, we formulate a parametric family of GPT models, where each model is governed by a trade-off parameter that balances the hallucination-related prediction error and the creativity of the model.
The Mathematical Framework: Probability Theory, Information Theory, and Optimization
This analysis of GPT models is grounded in a rigorous foundation of probability theory, information theory, and optimization. This allows us to uncover deep insights into the nature of hallucination in these models. By quantifying the trade-offs between hallucination and creativity, we pave the way for the development of more robust and versatile GPT models capable of handling diverse tasks with improved performance.
Training GPT Models: Learning from the Past
The training of GPT models involves learning the conditional probabilities for all tokens in the vocabulary and all possible positions. This is akin to learning a new language, where understanding the meaning of a sentence depends on the words that came before. GPT employs a part of transformer architectures, which consists of self-attention mechanisms, position-wise feed-forward networks, and layer normalization, to achieve this.
Deep Learning and GPT Models: A Closer Look
A GPT model, a variant of the transformer model, is composed of several identical layers, each containing a multihead self-attention mechanism and a position-wise feedforward neural network. This is similar to the way our brain processes information, with different regions responsible for different tasks.
The multihead self-attention mechanism can be thought of as the model’s ability to focus on different parts of the input simultaneously. The position-wise feed-forward network, on the other hand, is akin to a two-layer neural network with ReLU activation, which introduces non-linearity into the model, enabling it to learn complex patterns.
A Real-Life Example
Consider a GPT model trained to generate news articles. Given the first few sentences of an article about a recent football match, the model uses its understanding of the language and the context to generate the rest of the article. However, if the model starts to ‘hallucinate’, it might start writing about a player scoring a goal who wasn’t even playing in the match. This is where the trade-off between hallucination and creativity comes into play. While creativity is necessary for generating engaging content, too much of it can lead to hallucination, resulting in contextually implausible outputs.
The Mathematical Background
The mathematical underpinnings of GPT models are rooted in deep learning principles and the transformer architecture. These models are designed to learn hierarchical representations from input data by minimizing a loss function that quantifies the discrepancy between the model’s predictions and the ground truth.
Deep Learning Models
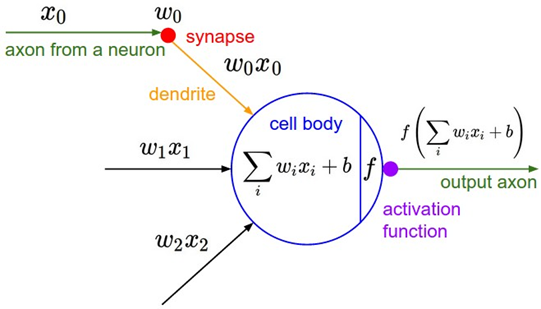
Deep learning models are a class of machine learning models that consist of multiple layers of interconnected artificial neurons. A deep learning model f : X → Y is a function that maps input data from a space X to a target space Y. The model is composed of L layers, and each layer l ∈ {1, . . . , L} consists of a set of neurons where k l is the number of neurons in layer l.
For each neuron n l i ∈ N l , let a l i denote its pre-activation value and z l i denote its post-activation value. The pre-activation value is a linear combination of the outputs from the neurons in the previous layer, and the post-activation value is obtained by applying the activation function to the pre-activation value:
a l i = ∑ j=1 k l-1 w l ij z l-1 j + b l i
z l i = σ(a l i)
where w l ij is the weight connecting neuron n l-1 j to neuron n l i , and b l i is the bias term for neuron n l i . In this context, σ(•) represents the activation function. A deep learning model can be viewed as a composition of functions f = f L ◦ f L-1 ◦ . . . ◦ f 1 where each function f l : R k l-1 → R k l represents the operation performed by layer l. The model’s parameters, Θ = {W l , b l } L l=1 , where W l ∈ R k l ×kl-1 is the weight matrix for layer l and b l ∈ R k l is the bias vector for layer l, are optimized by minimizing a loss function L(Θ; D), where D denotes the training dataset.
Generative Pre-Trained Transformer
A GPT model is composed of several layers of neural network modules, each consisting of layer normalization, multi-head attention, and dropout functionalities. The model integrates L number of transformer blocks, each of which houses a residual module encapsulating layer normalization, multi-head attention, dropout, and a fully connected layer. This systematic arrangement and interaction of modules and layers contribute to the robust performance of the GPT model.
Given an input sequence of tokens x = (x 1 , x 2 , . . . , x T ), where x t ∈ X for t = 1, 2, . . . , T, the GPT model learns a probability distribution P(x t |x <t ) over the vocabulary X , which is conditioned on the preceding tokens x <t = (x 1 , x 2 , . . . , x t-1 ). The conditional probability distribution P(x t |x <t ) estimated by a GPT can be represented by:
P(x t |x <t ) = softmax(W o z t )
where W o ∈ R |X|×d is the output weight matrix, and z t ∈ R d is the output of the t-th position in the final layer.
The GPT model utilizes a technique called positional encoding, which adds a fixed sinusoidal encoding to the input embeddings. The positional encoding function PE : N × N → R computes the position encoding for each position p ∈ N and each dimension i ∈ N in the input embedding space as follows:
PE(p, 2i) = sin(p/10000^(2i/d))
PE(p, 2i + 1) = cos(p/10000^(2i/d))
The GPT model employs layer normalization, which is applied to the input of both the multi-head self-attention and position-wise feedforward sublayers. Layer normalization helps alleviate the vanishing and exploding gradient problems and accelerates training. Given an input matrix H ∈ R T×d , layer normalization computes the normalized output matrix Ĥ ∈ R T×d as follows:
Ĥ = (H – μ(H))/sqrt(σ^2(H) + ε)
where μ(H) and σ^2(H) are the mean and variance of the j-th feature across all positions, respectively, and ε > 0 is a small constant for numerical stability.
The scaled dot-product attention function Attention : R T×d × R T×d × R T×d → R T×d takes as input a query matrix Q ∈ R T×d , a key matrix K ∈ R T×d , and a value matrix V ∈ R T×d , and it computes the output as follows:
Attention(Q, K, V) = softmax(QK^T/√d)V
where √d is a scaling factor that prevents the dot products from becoming too large.
In addition to the scaled dot-product attention mechanism, the GPT model employs the multi-head attention mechanism to capture different aspects of the input sequence. By having multiple attention heads, the model can learn different types of relationships between tokens in parallel. In conclusion, the GPT model is a powerful tool for generating contextually relevant and coherent text. It is based on the transformer architecture and uses a variety of mathematical functions and techniques to calculate the probability of the next word given the previous words. The model’s impressive language generation capabilities are a testament to the power of mathematics in advancing the field of AI.
This article is inspired by the papers.
1. “A Mathematical Investigation of Hallucination and Creativity in GPT Models” by Minhyeok Lee.
2. “A Mathematical Interpretation of Autoregressive Generative Pre-Trained Transformer and Self-Supervised Learning” by Minhyeok Lee.